O método da
falsa posição foi empregado para resolver equações lineares a partir de um "chute inicial".
Neste período a incógnita
x era chamada de
"aha" e o método consistia da escolha de um número arbitrário
como valor para
x. A partir deste valor a "expressão à esquerda" era computada e seu resultado comparado ao
"lado direito" da mesma. Para finalizar, calculava-se um fator de correção para obter o valor correto para a incógnita
x satisfazer a experssão original.
O problema 25 do
papiro Rhind, por exemplo, consiste na determinaçào de uma quantidade
sabendo que esta quantidade e sua metade somam 16. Ou seja, em notação atual o problema 25 equivale a
equação linear
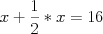
.
Para se resolver esta equação pelo
método da falsa posição deve-se inicialmente escolher um valor qualquer
para
x (
"aha"), digamos
x = 2. Com este valor computa-se a expressão
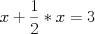
.
Deste modo o fator de correção deve ser
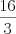
, pois este vezes
3 resulta o lado direito da equação original
(
16), ou seja, o valor correto de
"aha", ou
x, deve ser
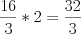
.




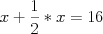 .
Para se resolver esta equação pelo método da falsa posição deve-se inicialmente escolher um valor qualquer
para x ("aha"), digamos x = 2. Com este valor computa-se a expressão
.
Para se resolver esta equação pelo método da falsa posição deve-se inicialmente escolher um valor qualquer
para x ("aha"), digamos x = 2. Com este valor computa-se a expressão 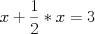 .
Deste modo o fator de correção deve ser
.
Deste modo o fator de correção deve ser 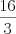 , pois este vezes 3 resulta o lado direito da equação original
(16), ou seja, o valor correto de "aha", ou x, deve ser
, pois este vezes 3 resulta o lado direito da equação original
(16), ou seja, o valor correto de "aha", ou x, deve ser 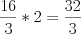 .
.