O primeiro a ver que o conceito de grupo, implícito nos grupos de permutações podia ser formulado num contexto bem mais abstrato foi
Arthur Cayley (1821-1895).
Ele tinha realmente uma visão abstrata da matemática e realizou diversas descobertas que contribuíram a levar a álgebra na direção de uma abstração crescente. Entre outras coisas, definiu os octonios (também descobertos independentemente por John T. Graves) que constituem o primeiro exemplo de anel não associativo e foi quem introduziu o conceito de matriz, que descobriu ao estudar invariantes de formas quadráticas.
Ele leu os trabalhos de
Cauchy de 1844-1846 e reconheceu nestes a possibilidade de uma visão mais abstrata. Em 1854 publicou, na Philosophical Magazine, um artigo intitulado
On the Theory of Groups as depending on the Symbolical Equation 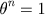
. Como a terminologia da teoria de conjuntos não era ainda usual na época de Cayley, ele iniciou seu trabalho tentando deixar claro que está lidando com símbolos abstratos e não com objetos concretos, como permutações ou números, e frizando que a operação considerada é associativa, mas não necessariamente comutativa:
...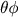 é naturalmente diferente de
é naturalmente diferente de 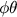 . Mas os símbolos
. Mas os símbolos 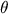 ,
, 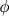 ,...em geral são tais que
,...em geral são tais que 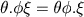 , etc, de forma tal que
, etc, de forma tal que 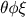 ,
, 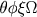 , etc., tem um significado definido, independente do modo particular de compor os símbolos.
, etc., tem um significado definido, independente do modo particular de compor os símbolos.
|
Logo em seguida enfatiza o fato de que está trabalhando com uma única operação:
Não é necessário (mesmo que isso pudesse ser feito) atribuir qualquer significado a um símbolo tal como 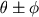 , ou ao símbolo 0, nem conseqüentemente a uma equação tal como
, ou ao símbolo 0, nem conseqüentemente a uma equação tal como 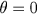 ou
ou 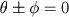 .
.
|
Sua definição de grupo é a seguinte:
Um conjunto de símbolos 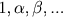 todos eles diferentes, tal que o produto de dois quaisquer deles (não importa em que ordem), ou o produto de qualquer um deles por si mesmo, pertence ao conjunto, diz-se que é um grupo.
todos eles diferentes, tal que o produto de dois quaisquer deles (não importa em que ordem), ou o produto de qualquer um deles por si mesmo, pertence ao conjunto, diz-se que é um grupo.
|
Imediatamente, ele faz uma observação que implica no resultado que, na linguagem atual, afirma que
todo grupo é isomorfo a um grupo de permutações e que hoje é conhecido como
Teorema de Cayley:
| Segue que, se todo o grupo é multiplicado por um qualquer dos seus símbolos, tanto como primeiro como segundo fator, o efeito é simplesmente reproduzir o grupo...
|
Ele passa então a discutir alguma das propriedades de grupos, introduz a Tabela da operação de grupo, hoje chamada por alguns de
Tabela de Cayley do grupo e observa:
A distinção entre a teoria da equação simbólica 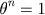 e aquela da equação ordinária
e aquela da equação ordinária 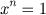 , se apresenta já no caso muito simples de n=4.
, se apresenta já no caso muito simples de n=4.
|
Fazendo uma análise das possíveis tabelas de operação num conjunto de quatro elementos ele mostra que existem dois grupos
"essencialmente diferente": (na nossa terminologia atual) o grupo cíclico de ordem 4 que "
é análogo ao sistema de raízes da equação 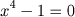
" e o chamado Grupo de Klein. Observa ainda que:
| Sistemas desta forma são de ocorrência freqüente na análise, e é apenas devido a sua extrema simplicidade que não foram notados expressamente.
|
Logo em seguida da alguns exemplos de "sistemas desta forma": isto é, de grupos isomorfos ao grupo de Klein.
Este trabalho de Cayley, na verdade, passou desapercebido para seus contemporâneos; como aponta M. Kline: "abstrações prematuras caem em ouvidos surdos tanto quando pertencem a matemáticos como a estudantes".
Novas definições abstratas de
grupo foram dadas posteriormente por H. Weber, em 1822 e, nesse mesmo ano por W. von Dyck.




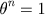 . Como a terminologia da teoria de conjuntos não era ainda usual na época de Cayley, ele iniciou seu trabalho tentando deixar claro que está lidando com símbolos abstratos e não com objetos concretos, como permutações ou números, e frizando que a operação considerada é associativa, mas não necessariamente comutativa:
. Como a terminologia da teoria de conjuntos não era ainda usual na época de Cayley, ele iniciou seu trabalho tentando deixar claro que está lidando com símbolos abstratos e não com objetos concretos, como permutações ou números, e frizando que a operação considerada é associativa, mas não necessariamente comutativa:
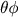 é naturalmente diferente de
é naturalmente diferente de 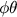 . Mas os símbolos
. Mas os símbolos 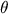 ,
, 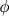 ,...em geral são tais que
,...em geral são tais que 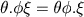 , etc, de forma tal que
, etc, de forma tal que 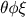 ,
, 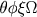 , etc., tem um significado definido, independente do modo particular de compor os símbolos.
, etc., tem um significado definido, independente do modo particular de compor os símbolos.
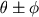 , ou ao símbolo 0, nem conseqüentemente a uma equação tal como
, ou ao símbolo 0, nem conseqüentemente a uma equação tal como 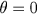 ou
ou 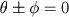 .
.
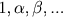 todos eles diferentes, tal que o produto de dois quaisquer deles (não importa em que ordem), ou o produto de qualquer um deles por si mesmo, pertence ao conjunto, diz-se que é um grupo.
todos eles diferentes, tal que o produto de dois quaisquer deles (não importa em que ordem), ou o produto de qualquer um deles por si mesmo, pertence ao conjunto, diz-se que é um grupo.
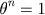 e aquela da equação ordinária
e aquela da equação ordinária 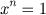 , se apresenta já no caso muito simples de n=4.
, se apresenta já no caso muito simples de n=4.
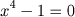 " e o chamado Grupo de Klein. Observa ainda que:
" e o chamado Grupo de Klein. Observa ainda que: