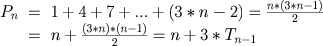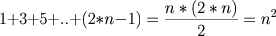Os pitagoricos desejavam compreender a natureza íntima dos números, então elaboraram os
números figurados que são números expressos como reunião de pontos numa determinada configuração geométrica, isto é, a quantidade de pontos representa um número, e estes são agrupados de formas geométricas sugestivas.
Os diagramas abaixo trazem alguns
números figurados.
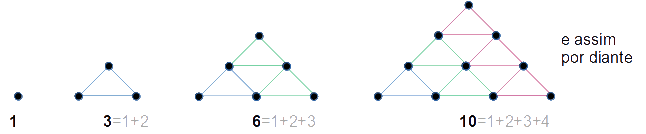 números triangulares
números triangulares
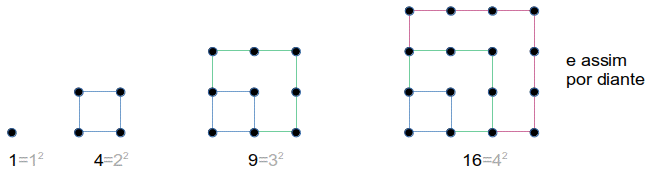 números quadrados
números quadrados
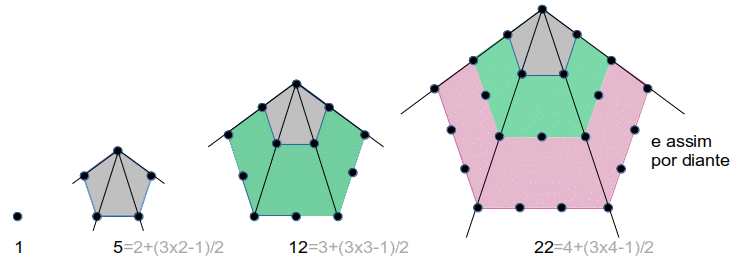 números pentagonais
números pentagonais
Enunciaremos e provaremos alguns teoremas relativos a
números figurados, como era feito pelos pitagóricos:
- Teorema I: O número triangular
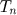 é igual à soma dos n primeiros inteiros positivos.
é igual à soma dos n primeiros inteiros positivos.
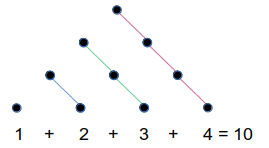
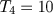
- Teorema II: Todo número quadrado é a soma de dois números triangulares sucessivos.
Observamos que um número quadrado na sua forma geométrica, pode ser dividido como na figura abaixo.
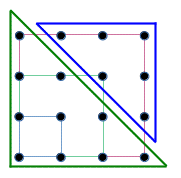
Vamos fazer a prova do teorema algebricamente. Seja o enésimo número triangular
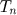
, dado pela soma da progressão aritmética,
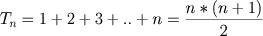 ,
,
seja o enésimo número quadrado
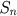
igual à
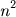
. Temos
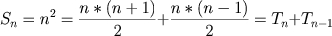
- Teorema III: o enésimo número pentagonal é igual a n mais três vezes o (n-1) - ésimo número triangular.

Seja o enésimo número pentagonal,
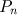
, dado pela soma de uma progressão aritmética.
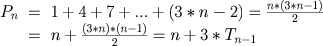
- Teorema III: A soma dos n primeiros inteiros ímpares, começando com 1, é o quadrado de n.
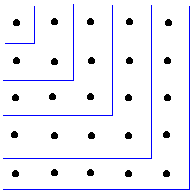
Calculando a soma da progressão aritmética, temos:
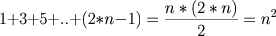
que demonstra o teorema.







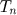 é igual à soma dos n primeiros inteiros positivos.
é igual à soma dos n primeiros inteiros positivos.

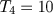

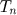 , dado pela soma da progressão aritmética,
, dado pela soma da progressão aritmética,
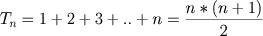 ,
, 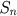 igual à
igual à 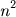 . Temos
. Temos
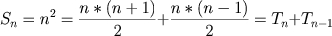

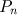 , dado pela soma de uma progressão aritmética.
, dado pela soma de uma progressão aritmética.