Um número se diz perfeito se é igual à soma de seus divisores próprios. Divisores próprios de um número positivo N são todos os divisores inteiros positivos de N exceto o próprio N.

Por exemplo, o número 6, seus divisores próprios são 1, 2 e 3, cuja soma é igual à 6.

1 + 2 + 3 = 6

Outro exemplo é o número 28, cujos divisores próprios são 1, 2, 4, 7 e 14, e a soma dos seus divisores próprios é 28.

1 + 2 + 4 + 7 + 14 = 28

Houve uma aura mística em torno dos números perfeitos, tentava-se uma conexão entre a teoria dos números e a Teologia. Santo Agostinho (354 - 430 d.C.) apresenta uma argumentação para esta conexão: "Seis é um número perfeito em si mesmo, e não porque Deus tenha criado todas as coisas em seis dias; o inverso é que é verdade: Deus criou todas as coisas em seis dias porque este número é perfeito, e teria sido perfeito mesmo que a obra dos seis dias não existisse".*

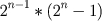
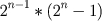A ultima proposição do nono livro dos Elementos de Euclides prova que se é um número primo então é um número perfeito, e estes números são pares. Euler provou que todo número perfeito par tem essa forma.

A existência ou não de números perfeitos ímpares é um desafio para a Teoria dos Números. Todos os números perfeitos menores que 5 000 já foram encontrados. Mas para números perfeitos maiores que 5 000 até 1985 totalizava 30 conhecidos.