- Dado
um triângulo ABC, seja
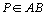 o pé da bissetriz pelo vértice C.
Determinar o lugar geométrico dos pontos X do plano ABC
tais que a bissetriz por X, do triângulo ABX,
passa por P. o pé da bissetriz pelo vértice C.
Determinar o lugar geométrico dos pontos X do plano ABC
tais que a bissetriz por X, do triângulo ABX,
passa por P.
Solução:
Pelo
teorema da bissetriz interna, um ponto X do plano ABC
é tal que a bissetriz do triângulo ABX por
X passa por P se e somente se 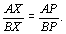
Logo,
pelo problema 170 da RPM 42, o lugar geométrico pedido
é a reta mediatriz de AB se AP=BP ou uma
circunferência se AP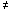 BP. BP.
(Solução
enviada por vários leitores.)
- Mostrar
que, reunindo os pontos médios dos lados de um quadrilátero ABCD
(convexo ou não), obtém-se um paralelogramo cuja área é a metade
da área do quadrilátero. Vale o mesmo para o "quadrilátero" ABCD
da figura da direita?
Solução:
Em
qualquer dos casos, MNPQ é um paralelogramo (podendo
ser degenerado), já que 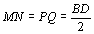 e e 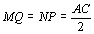 . .
Na
figura da esquerda temos:
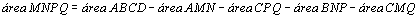
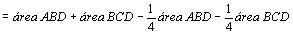
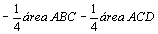
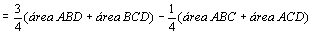
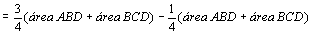
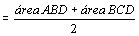 . .
Portanto,
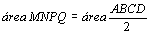 . .
Na
figura do meio temos:
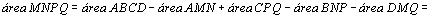
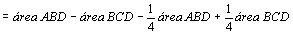 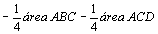
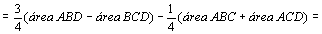
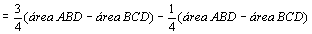
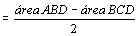 . .
Portanto,
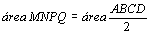 . .
Na
figura da direita temos:
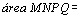
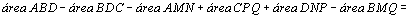
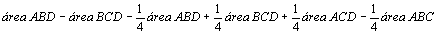 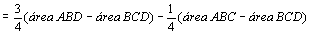
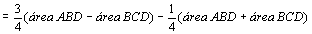
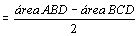 . .
Assim,
se definirmos, neste caso, a área MNPQ como sendo a diferença
das áreas dos triângulos ABD e BCD, teremos 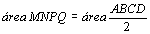 . .
- Na
loteria de Truchilândia, cada bilhete tem um número de três algarismos
que usa somente os algarismos 1, 2, 3 (é permitido repetir os
dígitos). Um bilhete é ganhador se coincide em pelo menos duas
posições com o número sorteado.
- Qual
é a probabilidade de que um apostador, que comprou um único bilhete,
ganhe o prêmio?
- Você
decide comprar 3 bilhetes. Que bilhetes você escolheria de modo
a maximizar sua probabilidade de ganhar o prêmio?
- Qual
é o número mínimo de bilhetes que você precisa comprar para ter
certeza que você ganhará o prêmio?
Solução:
Vamos
observar inicialmente que, como os números podem ser repetidos,
um sorteio dessa loteria admite 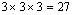 resultados possíveis. resultados possíveis.
a)
Um único jogo (por exemplo 121) garante a vitória do apostador em
sete resultados. De fato, as duas primeiras posições (12) garantem
a vitória se os resultados forem 121, 122, 123. A primeira e terceira
posições (1-1) permitem que o apostador ganhe com os resultados
111, 121, 131. Finalmente, a segunda e terceira posições
(21) darão a vitória com os resultados 121, 221, 321. Como o próprio
jogo é repetido duas vezes, são sete os resultados distintos favoráveis
ao jogador. Conclui-se, portanto, que a probabilidade de vitória
de um apostador que comprou um único bilhete é igual a 7/27.
b)
Com três bilhetes, o máximo que se pode esperar é garantir a vitória
em 21 jogos, o que nos daria uma probabilidade de vitória igual
a 7/9. Isso pode ser conseguido com jogos que não repitam nenhum
número na mesma posição. Assim, por exemplo, os conjuntos de três
jogos 111, 222, 333 e 123, 231, 312 dão ao jogador essa probabilidade
máxima de vitória.
c)
Como no total existem 27 resultados possíveis e cada jogo garante
a vitória do apostador em apenas sete, conclui-se que três jogos
não são suficientes para que tenhamos certeza da vitória. Mostraremos
a seguir que quatro jogos também não são suficientes. Como são três
algarismos e quatro jogos, existem dois algarismos que vão aparecer
uma única vez na primeira posição. Vamos supor que o número 1 apareça
em um único jogo na primeira posição. É fácil ver que esse jogo
garante a vitória do apostador em cinco jogos distintos que começam
com o número 1. Existem nove jogos que começam com o número 1 e
a vitória nos outros quatro terá que ser garantida pelos algarismos
que aparecem na segunda e terceira posições dos demais jogos. Como
só existem três outros jogos, sobra um jogo que começa com 1, que
se for sorteado não dará a vitória ao apostador.
Existem
vários conjuntos de cinco jogos que resolvem o problema, como o
leitor pode verificar nos exemplos:
123,
211, 232, 312, 331; 121, 132, 213, 322, 331.
(Adaptada
da solução publicada na revista Eureka, número 6.)
- Considere
o conjunto dos números inteiros de quatro algarismos
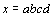 , onde a, b,
c e d são não nulos e não necessariamente distintos.
Seja , onde a, b,
c e d são não nulos e não necessariamente distintos.
Seja 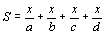 .
Para que valores de x, teremos .
Para que valores de x, teremos 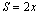 ? ?
Solução:
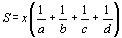 . Teremos . Teremos 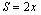 se e só se se e só se 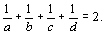 Vamos supor, sem perda de generalidade, que Vamos supor, sem perda de generalidade, que 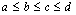 e tomemos inicialmente e tomemos inicialmente 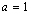 . Então, b será necessariamente
maior que 1, pois, caso b fosse igual a 1, a soma das quatro
frações seria maior que 2. . Então, b será necessariamente
maior que 1, pois, caso b fosse igual a 1, a soma das quatro
frações seria maior que 2.
Supondo
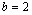 , temos que encontrar soluções para , temos que encontrar soluções para 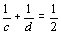 . .
Para
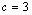 , obtemos , obtemos 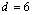 e, para e, para 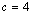 , d também será igual a 4. Obtemos assim duas soluções, que são
1236 e 1244. Para , d também será igual a 4. Obtemos assim duas soluções, que são
1236 e 1244. Para 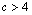 , , 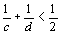 e, portanto,
não existe solução. e, portanto,
não existe solução.
Vamos
analisar agora o caso 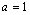 e e 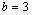 . Nesse caso, a única solução é dada por . Nesse caso, a única solução é dada por
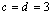 , que corresponde
a , que corresponde
a 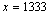 . Não é difícil verificar que não existe nenhuma outra solução se . Não é difícil verificar que não existe nenhuma outra solução se 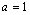 . .
Para
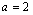 , temos que procurar soluções para , temos que procurar soluções para 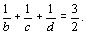 A única solução é dada por A única solução é dada por 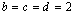 ,
que corresponde a ,
que corresponde a 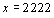 .
Não existem soluções para .
Não existem soluções para 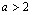 , pois, nesse caso, a soma das quatro frações
seria no máximo igual a 4/3. , pois, nesse caso, a soma das quatro frações
seria no máximo igual a 4/3.
Observamos
que todas as permutações das quatro soluções obtidas são também
soluções do problema, o que nos dá um total de 41 soluções.
(Adaptação
de soluções enviadas por vários leitores.)
Relação
dos leitores que enviaram soluções dos
problemas
da RPM 41
-
-
| Amadeu
Carneiro de Almeida, RJ - 174,175 |
João
Linneu do A. Prado, SP - 174 |
| Américo
Antônio Frigo, SP - 176, 177 |
José
Hernandez, SP - 177 |
| André
L. Souza de Araujo, RJ - 174 |
José
Renato C. Carneiro, SP - 175 |
| Carlos
A. S. Victor, RJ - 174,175, 176, 177 |
Lhioko
S. Tayra, SP - 162 |
| Dorival
Carmo de Sousa, GO - 174 |
Luciano
Marinho Filho, PE - 175, 177 |
| Eudes
Antônio da Costa, GO - 174 |
Ronaldo
Antonio dos Santos, GO - 174 |
| F.
W. Leão, RJ - 174, 175, 177 |
Trajano
Pires da Nóbrega Neto, SP - 177 |
| Fernando
Carvalho Ramos, RS - 177 |
Tsunediro
Takahaski, SP - 175, 177 |
| Florival
Carmo de Souza, GO - 174 |
Wanderley
Gamba, SP - 174 |
| Geraldo
Perlino Junior, SP - 174, 175, 177 |
|
|


