O fato de que um número negativo não tem raiz quadrada parece ter sido
sempre claro para os matemáticos que se depararam com a questão.
As equações de segundo grau apareceram na matemática já nas tabuletas de
argila da Suméria, aproximadamente 1700 anos antes de Cristo e,
ocasionalmente, levaram a radicais de números negativos; porém, não foram
elas, em momento algum, que sugeriram o uso de números complexos.
A rigor, uma equação era vista como a formulação matemática de um problema
concreto; assim, se no processo de resolução aparecia uma raiz quadrada de
um número negativo, isto era interpretado apenas como uma indicação de que o
problema originalmente proposto não tinha solução. Como veremos neste
capítulo, foram só as equações de terceiro grau que impuseram a necessidade
de trabalhar com estes números.
Vejamos inicialmente alguns antecedentes. Um primeiro exemplo desta atitude
aparece na
Arithmetica de Diophanto. Aproximadamente no ano de 275
d.c. ele considera o seguinte problema:
Um triângulo retângulo tem área igual a 7 e seu perímetro é de 12
unidades. Encontre o comprimento dos seus lados.
Chamando
x e
y o comprimento dos catetos desse triângulo
temos, na nossa notação atual:
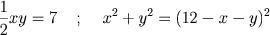 .
.
Substituindo
y em função de
x obtemos a equação:
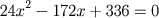 ,
,
cujas raízes são:
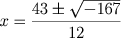 .
.
Neste ponto
Diophanto observa que só poderia haver solução se
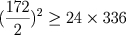
o que implica, obviamente, que não
existe o triângulo procurado. Neste contexto, é claro que não há
necessidade alguma de introduzir um sentido para a expressão
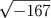
.
Outras referências à questão aparecem na matemática indiana. Aproximadamente
no ano 850 d.c., o matemático indiano
Mahavira afirma:
... como na natureza das coisas um negativo não é um quadrado, ele não tem portanto raiz quadrada.
Já no século XII o famoso matemático
Bhaskara (1114-1185 aprox.) escreve:
O quadrado de um positivo é positivo; e a raiz quadrada de um positivo é
dupla: positiva e negativa. Não há raiz quadrada de um negativo; pois ele não é um quadrado.
Também na matemática européia aparecem observações desta natureza,
Luca Paccioli, na sua
Summa di Arithmetica Geometria, publicada em 1494,
escreve que a equação
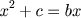
é solúvel somente se
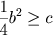
e o matemático francês Nicolas Chuquet (1445-1500 aprox.) faz observações
semelhantes sobre ``soluções impossíveis'' num manuscrito não publicado de 1484.
Desde que os
babilônios descobriram a forma de resolver equações
quadráticas, se passaram mais de 3000 anos até a descoberta da fórmula que
da as raízes das equações de terceiro grau por Del Ferro,
Cardano e
Tartaglia no início do século XVI. Dada a equação
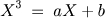
, a fórmula
de Cardano-Tartaglia que permite obter uma raiz é:
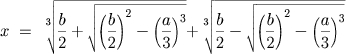 .
.
Esta fórmula, junto com o método de resolução das equações de quarto grau,
foi dada a público em 1545, no
Ars Magna, de Cardano. A publicação
desta obra deu um novo impulso ao estudo da álgebra.
É claro que quando
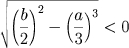
a fórmula
parece não ter sentido: porém, mesmo neste caso, a equação pode ter solução.
Em 1575, um outro algebrista italiano chamado
Raphael Bombelli publicou um
livro chamado
Álgebra em que descreve as idéias de Cardano de forma
didática. é precisamente neste livro onde aparece pela primeira vez a
necessidade explícita de introduzir os números complexos e também uma
primeira apresentação do assunto.
Ao aplicar a fórmula acima ao exemplo
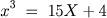
, Bombelli obtém:
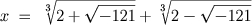 ,
,
mas é facil perceber diretamente que
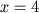
é uma solução desta equação.
Bombelli decidiu trabalhar como se
raízes quadradas de números negativos
fossem verdadeiros números. Ele concebe que a raiz cúbica de
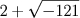
pode ser um ``número'' da mesma forma, isto é, do tipo
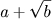
. Talvez, a raiz cúbica de
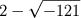
seja da forma
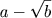
. Neste caso, ter-se-ia que
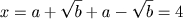
,
donde é fácil deduzir que
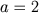
. Assumindo que se aplicam a estes números
as regras usuais dos cálculos algébricos não foi difícil descobrir que
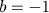
e verificar que, de fato,
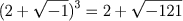 .
.
Bombelli percebeu claramente a importância deste achado. Ele diz:
|
Eu achei uma espécie de raiz cúbica muito diferente das outras, que aparece
no capítulo sobre o cubo igual a uma quantidade e um número. ... A
princípio, a coisa toda me pareceu mais baseada em sofismas que na verdade,
mas eu procurei até que achei uma prova.
|
O caso em que
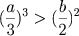
, era chamado na época de
casus irreducibilis porque qualquer tentatica de calcular de fato o
valor da incógnita pela fórmula de Cardano-Tartaglia, sem conhece-lo
antecipadamente leva, de novo, à equação de terceiro grau original. Porém,
este era, em certo sentido, o mais importante de todos, pois é justamente o
caso em que a equação considerada tem três raízes reais.
Faremos aqui um pequeno resumo da evolução dos números complexos, para que o
leitor tenha uma visão global da história do assunto.
- O símbolo
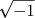 foi introduzido em 1629 por Albert Girard.
foi introduzido em 1629 por Albert Girard.
- O símbolo i foi usado pela primeira vez para representar
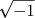 por Leonhard Euler em 1777, apareceu impresso pela primeira vez em 1794 e se tornou amplamente aceito após seu uso por Gauss em 1801.
por Leonhard Euler em 1777, apareceu impresso pela primeira vez em 1794 e se tornou amplamente aceito após seu uso por Gauss em 1801.
- Os termos real e imaginário foram empregados pela primeira vez por René Descartes em 1637.
- A expressão número complexo foi introduzida por Carl Friederich Gauss em 1832.
- A representaçãp gráfica dos números complexos foi obtida independentemente por Caspar Wessel, em 1799; Jean-Robert Argand, em 1822 e
Carl Friederich Gauss, em 1831.
- A apresentação hoje usual dos números complexos como pares ordenados de números reais foi dada por Sir William Rowan Hamilton em 1837.




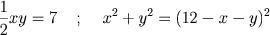 .
.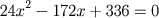 ,
,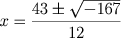 .
.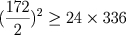 o que implica, obviamente, que não
existe o triângulo procurado. Neste contexto, é claro que não há
necessidade alguma de introduzir um sentido para a expressão
o que implica, obviamente, que não
existe o triângulo procurado. Neste contexto, é claro que não há
necessidade alguma de introduzir um sentido para a expressão 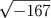 .
Outras referências à questão aparecem na matemática indiana. Aproximadamente
no ano 850 d.c., o matemático indiano Mahavira afirma:
.
Outras referências à questão aparecem na matemática indiana. Aproximadamente
no ano 850 d.c., o matemático indiano Mahavira afirma:
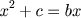 é solúvel somente se
é solúvel somente se 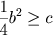 e o matemático francês Nicolas Chuquet (1445-1500 aprox.) faz observações
semelhantes sobre ``soluções impossíveis'' num manuscrito não publicado de 1484.
Desde que os babilônios descobriram a forma de resolver equações
quadráticas, se passaram mais de 3000 anos até a descoberta da fórmula que
da as raízes das equações de terceiro grau por Del Ferro, Cardano e
Tartaglia no início do século XVI. Dada a equação
e o matemático francês Nicolas Chuquet (1445-1500 aprox.) faz observações
semelhantes sobre ``soluções impossíveis'' num manuscrito não publicado de 1484.
Desde que os babilônios descobriram a forma de resolver equações
quadráticas, se passaram mais de 3000 anos até a descoberta da fórmula que
da as raízes das equações de terceiro grau por Del Ferro, Cardano e
Tartaglia no início do século XVI. Dada a equação 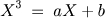 , a fórmula
de Cardano-Tartaglia que permite obter uma raiz é:
, a fórmula
de Cardano-Tartaglia que permite obter uma raiz é:
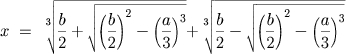 .
.
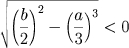 a fórmula
parece não ter sentido: porém, mesmo neste caso, a equação pode ter solução.
Em 1575, um outro algebrista italiano chamado Raphael Bombelli publicou um
livro chamado Álgebra em que descreve as idéias de Cardano de forma
didática. é precisamente neste livro onde aparece pela primeira vez a
necessidade explícita de introduzir os números complexos e também uma
primeira apresentação do assunto.
Ao aplicar a fórmula acima ao exemplo
a fórmula
parece não ter sentido: porém, mesmo neste caso, a equação pode ter solução.
Em 1575, um outro algebrista italiano chamado Raphael Bombelli publicou um
livro chamado Álgebra em que descreve as idéias de Cardano de forma
didática. é precisamente neste livro onde aparece pela primeira vez a
necessidade explícita de introduzir os números complexos e também uma
primeira apresentação do assunto.
Ao aplicar a fórmula acima ao exemplo 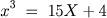 , Bombelli obtém:
, Bombelli obtém:
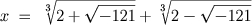 ,
,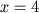 é uma solução desta equação.
Bombelli decidiu trabalhar como se raízes quadradas de números negativos
fossem verdadeiros números. Ele concebe que a raiz cúbica de
é uma solução desta equação.
Bombelli decidiu trabalhar como se raízes quadradas de números negativos
fossem verdadeiros números. Ele concebe que a raiz cúbica de
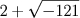 pode ser um ``número'' da mesma forma, isto é, do tipo
pode ser um ``número'' da mesma forma, isto é, do tipo
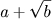 . Talvez, a raiz cúbica de
. Talvez, a raiz cúbica de 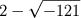 seja da forma
seja da forma
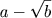 . Neste caso, ter-se-ia que
. Neste caso, ter-se-ia que 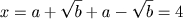 ,
donde é fácil deduzir que
,
donde é fácil deduzir que 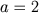 . Assumindo que se aplicam a estes números
as regras usuais dos cálculos algébricos não foi difícil descobrir que
. Assumindo que se aplicam a estes números
as regras usuais dos cálculos algébricos não foi difícil descobrir que
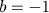 e verificar que, de fato,
e verificar que, de fato,
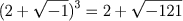 .
.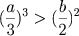 , era chamado na época de
casus irreducibilis porque qualquer tentatica de calcular de fato o
valor da incógnita pela fórmula de Cardano-Tartaglia, sem conhece-lo
antecipadamente leva, de novo, à equação de terceiro grau original. Porém,
este era, em certo sentido, o mais importante de todos, pois é justamente o
caso em que a equação considerada tem três raízes reais.
Faremos aqui um pequeno resumo da evolução dos números complexos, para que o
leitor tenha uma visão global da história do assunto.
, era chamado na época de
casus irreducibilis porque qualquer tentatica de calcular de fato o
valor da incógnita pela fórmula de Cardano-Tartaglia, sem conhece-lo
antecipadamente leva, de novo, à equação de terceiro grau original. Porém,
este era, em certo sentido, o mais importante de todos, pois é justamente o
caso em que a equação considerada tem três raízes reais.
Faremos aqui um pequeno resumo da evolução dos números complexos, para que o
leitor tenha uma visão global da história do assunto.
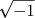 foi introduzido em 1629 por Albert Girard.
foi introduzido em 1629 por Albert Girard.
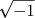 por Leonhard Euler em 1777, apareceu impresso pela primeira vez em 1794 e se tornou amplamente aceito após seu uso por Gauss em 1801.
por Leonhard Euler em 1777, apareceu impresso pela primeira vez em 1794 e se tornou amplamente aceito após seu uso por Gauss em 1801.